複素関数を色でプロットするツール（説明）

f(z) =

→

関数：
変数には複素数zのほか、\(z = x+i y = r\mathrm{e}^{i t}\) としたときの実数x、y、r、tが使えます。tの範囲は \(-\pi ≦ t ≦ \pi\) です。
変数は実数zです。
2*zや3*iなど、乗算には*が必須です。
使用可能な定数と関数は次の通り：隠す
  • 定数
    • e
    自然対数の底 \(\mathrm{e}=2.71828...\) です。
    pi
    円周率 \(\pi=3.14159...\) です。
    i
    虚数単位 \(i=\sqrt{-1}\) です。
    w
    \(w=-\frac{1}{2}+\frac{\sqrt{3}}{2}i\) です。これは \(w^3=1\) の解の1つで、他の2つは \(1,-w-1\) と表せます。
  • 複素数のプロパティ
    • re(c)
    複素数cの実部を返します。c=zの場合、xと等値です。
    im(c)
    複素数cの虚部を返します。c=zの場合、yと等値です。
    abs(c)
    複素数cの絶対値を返します。c=zの場合、rと等値です。
    arg(c)
    複素数cの偏角 \(\theta\) を \(-\pi ≦ \theta ≦ \pi\) の範囲で返します。c=zの場合、tと等値です。負の実軸に沿った分岐切断（branch cut）を持ちます（負の実軸上で不連続です）。
  • 二項演算
    • +,-,*,/
    加減乗除です。
    ^
    複素数冪\(a^b\)です。pow(a,b)も同じ演算です。底aに関してlogと同じ分岐切断を持ちます。
  • 指数・対数関数
    • exp(c)
    底を \(\mathrm{e}\) とする指数関数 \(\mathrm{e}^c\) です。
    log(c)
    底を \(\mathrm{e}\) とする自然対数関数 \(\log_\mathrm{e}c\) です。 \(\mathrm{e}^w=c\) を満たす複素数 \(w\) は複数存在し、任意の整数 \(n\) を用いて \(w=\log_\mathrm{e}|c|+i(\arg(c)+2n\pi)\) と表せます。この関数は、それらのうち \(n=0\) である値を返します。そのため、返値の虚部は区間 \([-\pi,\pi]\) に属します。負の実軸に沿った分岐切断を持ちます。
    sqrt(c),cbrt(c)
    平方根 \(\sqrt{c}\) と、立方根 \(\sqrt[3]{c}\) です。logと同じ分岐切断を持ちます。
  • 三角関数とその逆関数
    • sin(c),cos(c),tan(c)
    三角関数の正弦 \(\sin c\) 、余弦 \(\cos c\) 、正接 \(\tan c\) です。
    asin(c),acos(c)
    逆正弦 \(\sin^{-1}c\) と逆余弦 \(\cos^{-1}c\) です。2つの分岐切断を持ち、実軸の \(|z|>1\) の部分に沿って \(±∞\) へと延びています。
    atan(c)
    逆正接 \(\tan^{-1}c\) です。2つの分岐切断を持ち、虚軸の \(|z|>1\) の部分に沿って \(±∞i\) へと延びています。
  • 双曲線関数とその逆関数
    • sinh(c),cosh(c),tanh(c)
    双曲線関数の正弦 \(\sinh c\) 、余弦 \(\cosh c\) 、正接 \(\tanh c\) です。
    asinh(c)
    逆双曲線正弦 \(\sinh^{-1}c\) です。2つの分岐切断を持ち、虚軸の \(|z|>1\) の部分に沿って \(±∞i\) へと延びています。
    acosh(c)
    逆双曲線余弦 \(\cosh^{-1}c\) です。分岐切断を1つ持ち、 \(1\) から実軸に沿っての負の方向へ \(-∞\) へと延びています。
    atanh(c)
    逆双曲線正接 \(\tanh^{-1}c\) です。2つの分岐切断を持ち、実軸の \(|z|>1\) の部分に沿って \(±∞\) へと延びています。
  • その他の関数（使用には注意が必要です）
    • zeta(c)
    リーマンゼータ関数です。非常に時間が掛かり、特に虚部が負である領域で重いです。また途中で打ち切る影響で、虚部がおよそ-7未満の領域では計算がうまくできず、およそ0を返してしまいます。Wikipediaで綺麗な画像が見れます。
    mand(n,c)
    漸化式 \(z_{n+1} = z_n^2 + c, z_0 = 0\) における \(z_n\) の値を返します。nは非負整数です。
    複素数列 \(\{z_n\}\) が \(n \to \infty\) で無限大に発散しない複素数 \(c\) 全体の集合はマンデルブロ集合と呼ばれます。もしも mand(∞,z) が計算できれば、白以外の色でプロットされる領域です。実際にはmand(10,z)くらいでそれらしい図形が見えてきます。ただ、nが大きいと（n=10程度でも）計算が乱れやすくなります。
    julia(n,c,d)
    漸化式 \(z_{n+1} = z_n^2 + c, z_0 = d\) における \(z_n\) の値を返します。nは非負整数です。julia(n,c,0)はmand(n,c)と等価です。大きなnに関してはmandと同様に乱れやすいです。
定義域：
z = x + i*y として、
< \(x\)\(z\) <
< \(y\) <
実数部の値域：
< \(f_\mathbb{R}(z)\) <
定義域は以下のパラメーターから決定されます。
画像サイズ：
1ピクセルあたりの差分：


平行移動：
おまけ：
\(\mathbb{C}→\mathbb{C}\) 以外の関数でも遊べます。ただし簡易な実装であり、x-y平面のグラフについては点と点の間の補間をしないため飛び飛びになることがあります。
  • （実数の3つ組をRGBに対応させます）
  • （x-y平面のグラフを複素数で色塗りします）
  • （x-y平面のグラフをRGBで色塗りします）

説明

これは何？

複素関数を座標平面への着色としてプロットするツールです。定義域を表す座標平面の各点に、関数の値を表す色をプロットします。計算はブラウザ側（JavaScript）で行われるため、描画にかかる時間は閲覧環境に依存します。

なお、計算時間や精度についての最適化は行っていないので（たとえば複素関数は定義通りの式のまま実装されています）、応答が遅い、誤差で数値がおかしいなどの不具合が起こることがあります。あらかじめご了承ください。

プロットの例
\(z\)
\(\sin(z)\)
\(\log(z)\)
\(\mathrm{e}^z\)
\(z^3-1\)

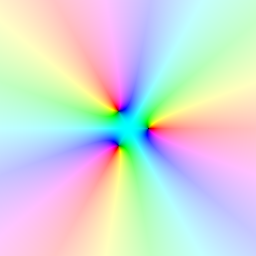
色の決め方

複素数の値に対して、絶対値から輝度、偏角から色相を決めて、HSL色空間で表します。彩度は100%で固定です。偏角から色相へは単純なラジアンから度への変換ですが、絶対値から輝度へは値の範囲が異なるので、次の関数 \(L:[0,∞)→[0\%,100\%)\) で変換をします。

\(L(r)=\begin{cases} \frac{1}{2}r^{\log_2\frac{\mathrm{e}}{4}}×100\% & (0≦r≦1)\\ (1-\frac{1}{2\log_2(\sqrt{r}+1)})×100\% & (1<r) \end{cases}\)

例えば、関数 \(f(z)=z^2\) は \(z=0+1\mathrm{i}\) のとき \(f(z)=-1=1\mathrm{e}^{\mathrm{i}\pi}\) です。 \(\pi=180°,L(1)=50\%\) ですから、点 \((0,1)\) に \((H,S,L)=(180°,100\%,50\%) \) の色をプロットすることになります。

おまけとして、3つの実数から色を決めるものも実装しました。各関数の実部の値を次の関数 \(R:(-∞,∞)→(0,256)\) で変換した後、3つの値の組 \((R,G,B)\) をRGB色空間に対応させます。

\(R(x)=\begin{cases} \frac{x}{|x|}(1-\frac{1}{2\log_2(|x|+2)})×256 \end{cases}\)

式の入力について

sin(z+pi)*exp(z^2)-iのように入力してください。入力フォームで一覧した通りの変数・定数・記号・関数が使えます。スペースや、大文字小文字の違い、括弧の違い（(),{},[]の3種類）は無視されます。全角文字は使えません。括弧の数のチェックなどはしていないので、きちんと閉じられているかなどは自分で確認してください。

「分岐切断」とは

複素数の偏角 arg(z) は \(-\pi ≦ \theta ≦ \pi\) の範囲*1で値を返すため、負の実軸を横切るときに値が \(2\pi\) だけ飛び、連続ではありません。このように不連続となる曲線をbranch cut（分岐切断）といいます（「分岐切断」という呼称はPython複素関数ライブラリのリドキュメントで使われていました）。logはargに依存するため同様の分岐切断を持ち、平方根・立方根・逆三角関数・逆双曲線関数は定義の中にlogがあるため、やはり分岐切断が生じます。

arg(c)+2*piとすれば \(2\pi\) だけ大きい偏角を得られることから、log(c)+i*2*piなどとすることで、logの別の分岐が得られます。

参考ウェブサイト

実装にあたって参考にした情報（の一部）です。

cmath --- 複素数のための数学関数 — Python 3.7.1 ドキュメント
逆双曲線関数と逆三角関数の branch cut|雑記帳
複素関数の実装で参考にしました。
シンプルな数式のパーサー（操車場アルゴリズム） - 藤 遥のブログ
操車場アルゴリズム - Wikipedia
入力された数式を実際に計算できる形に字句解析・構文解析する方法は、Wikipediaに掲載されている操車場アルゴリズムをそのまま実装しました。
リーマンのゼータ関数で遊び倒そう (Ruby編) - tsujimotterのノートブック
ゼータ関数はこのページの定義式で実装しました。